基于电磁场理论的电力电子换流回路本质解析

倾佳电子杨茜SiC碳化硅MOSFET销售团队认知培训资料 基于电磁场理论的电力电子换流回路本质解析

BASiC Semiconductor基本半导体一级代理商倾佳电子（Changer Tech）是一家专注于功率半导体和新能源汽车连接器的分销商。主要服务于中国工业电源、电力电子设备和新能源汽车产业链。倾佳电子聚焦于新能源、交通电动化和数字化转型三大方向，代理并力推BASiC基本半导体SiC碳化硅MOSFET单管，SiC碳化硅MOSFET功率模块，SiC模块驱动板等功率半导体器件以及新能源汽车连接器。

倾佳电子杨茜致力于推动国产SiC碳化硅模块在电力电子应用中全面取代进口IGBT模块，助力电力电子行业自主可控和产业升级！

倾佳电子杨茜咬住SiC碳化硅MOSFET功率器件三个必然，勇立功率半导体器件变革潮头：

倾佳电子杨茜咬住SiC碳化硅MOSFET模块全面取代IGBT模块和IPM模块的必然趋势！

倾佳电子杨茜咬住SiC碳化硅MOSFET单管全面取代IGBT单管和大于650V的高压硅MOSFET的必然趋势！

倾佳电子杨茜咬住650V SiC碳化硅MOSFET单管全面取代SJ超结MOSFET和高压GaN 器件的必然趋势！

1. 引言：电力电子学的范式转移——从电路到电磁场

电力电子技术的演进史，本质上是对电能控制精度与密度的不断追求史。在过去的几十年里，基于集总参数（Lumped Parameter）模型的电路理论（Circuit Theory）一直是分析和设计功率变换器的基石。工程师们习惯于将复杂的物理系统抽象为由理想开关、电阻、电感和电容通过无质量导线连接而成的拓扑结构，利用基尔霍夫电流定律（KCL）和电压定律（KVL）来求解电压与电流的稳态关系。这种方法在低频、低功率密度且开关速度较慢的硅基（Si）器件时代是行之有效的，也是极为成功的工程简化 。

然而，随着宽禁带（Wide Bandgap, WBG）半导体材料——如碳化硅（SiC）和氮化镓（GaN）——的广泛应用，电力电子技术进入了一个全新的“场”时代。器件的开关速度（dv/dt 和 di/dt）提升了整整一个数量级，开关频率从几十千赫兹跃升至兆赫兹频段。在纳秒级的开关瞬态过程中，信号的波长甚至可以与电路板的物理尺寸相比拟，传统的“导线”不再是简单的等电位连接体，而是复杂的传输线；“电感”不再仅仅是磁性元件的属性，而是所有回路的固有空间几何特征；“电流”也不再局限于导体内部的电荷流动，位移电流在绝缘介质中的穿透作用变得不可忽视 。

此时，电路理论的局限性暴露无遗。它无法解释为何完美的原理图设计在PCB上会出现无法消除的电压尖峰；无法解释为何隔离良好的电路之间会存在强烈的共模干扰；更无法直观地描述能量是如何在非导体区域（如PCB介质层）中流动的。为了触及换流回路的本质，我们必须打破集总参数的思维禁锢，回归到描述电磁现象的最基本法则——麦克斯韦方程组（Maxwell's Equations）和电磁场理论（Electromagnetic Field Theory） 。

倾佳电子从电磁场的微观视角，对电力电子中的核心物理过程——换流（Commutation） ——进行剖析。我们将不再把换流回路视为简单的电流通路，而是将其视为引导电磁波传播的波导结构、存储磁能的空间几何体以及辐射能量的天线系统。通过坡印廷矢量（Poynting Vector）分析能量的流动路径，通过位移电流（Displacement Current）解析噪声的耦合机制，通过近场（Near-field）与远场（Far-field）理论探讨电磁兼容性（EMI），从而为下一代高密度、高效率功率变换器的设计提供底层的物理洞察。

2. 物理基础：麦克斯韦方程组在电力电子中的演绎

要理解换流回路的本质，首先必须明确支配其行为的物理定律。在宏观尺度下，所有的电磁现象，无论是在巨大的电力传输线上，还是在微小的芯片封装内，都受到麦克斯韦方程组的绝对统治。对于电力电子工程师而言，这四个方程不仅仅是数学公式，更是换流回路中每一个寄生效应、每一次能量转换和每一处干扰源的物理根源 。

2.1 高斯定律与节点电场积聚

**高斯定律（Gauss's Law）**描述了电场与电荷分布的关系：

∮S​E⋅dA=ϵ0​Q​

在换流回路中，这一方程揭示了高压节点（High dv/dt Node）的本质。当开关器件（如MOSFET）处于关断状态或正在关断的瞬间，漏极（Drain）与源极（Source）之间承受高电压，这意味着在开关器件的结电容以及周围的PCB铜箔表面积聚了大量的电荷。

物理洞察： 高 dv/dt 实际上意味着空间电荷密度的剧烈变化。根据高斯定律，这种电荷的快速积累或消散必然伴随着周围空间电场分布的剧烈扰动。这种强时变电场是产生位移电流的源头，也是容性耦合（Capacitive Coupling）干扰的根本原因 。

2.2 高斯磁定律与磁通闭合性

**高斯磁定律（Gauss's Law for Magnetism）**指出自然界中不存在磁单极子：

∮S​B⋅dA=0

这意味着磁力线永远是闭合的。对于电力电子设计，这一推论至关重要：磁通必须形成回路。

物理洞察： 换流回路中的电流产生磁场，而这些磁力线必须在空间中找到闭合路径。磁力线路径的磁阻（Reluctance）决定了电感的大小。如果磁力线不得不穿过空气或其它的非磁性介质闭合，能量就会散布在更广阔的空间中，形成所谓的“漏磁”或“杂散场”，这正是邻近效应和电磁干扰的物理基础 。

2.3 法拉第定律与电压过冲的起源

**法拉第电磁感应定律（Faraday's Law of Induction）**描述了时变磁场如何产生电场：

∮C​E⋅dl=−dtdΦB​​=−dtd​∫S​B⋅dA

这是理解换流回路中“电压尖峰”的核心方程。在电路理论中，我们将电压视为标量电势差（Potential Difference），即 ΔV。但在时变磁场存在的换流瞬间，电场是非保守的（Non-conservative），此时“电压”的概念必须修正为感应电动势（EMF）。

物理洞察： 当MOSFET快速关断，回路电流（以及随之产生的磁通 ΦB​）迅速塌缩。根据法拉第定律，磁通的变化在回路导线周围的空间感应出一个旋涡状的电场。这个感应电场沿着回路积分，表现为开关两端的电压过冲（Voltage Overshoot）。因此，电压尖峰不是由电源产生的，而是由空间中原本存储的磁场能量在“反抗”电流变化时转化而来的电场能量 。

2.4 安培-麦克斯韦定律与换流的连续性

**安培-麦克斯韦定律（Ampère-Maxwell Law）**是分析高频换流最关键的方程，它引入了位移电流项：

∮C​B⋅dl=μ0​(Iencl​+ϵ0​dtdΦE​​)

其中，Iencl​ 是传导电流（Conduction Current），ϵ0​dtdΦE​​ 是位移电流（Displacement Current）。

物理洞察： 这一方程解决了开关断开时电流“去哪了”的问题。在开关导通时，传导电流占主导；当开关关断，物理触点断开，传导电流被切断，但由于开关两端电压迅速上升（dΦE​/dt 极大），位移电流接管了回路，维持了磁场的连续性。换流的本质，实际上是电流形态从电子流（传导）向电场变化流（位移）的剧烈转换 。

3. 换流回路的解剖学：拓扑、几何与“热回路”

在深入场分析之前，必须准确界定分析对象。在电力电子拓扑中，并非所有的导线都同等重要。只有那些在开关周期内电流发生剧烈突变（高 di/dt）的回路，才是电磁场分析的核心，工程上称之为“热回路”（Hot Loop）或“换流回路”（Commutation Loop）。

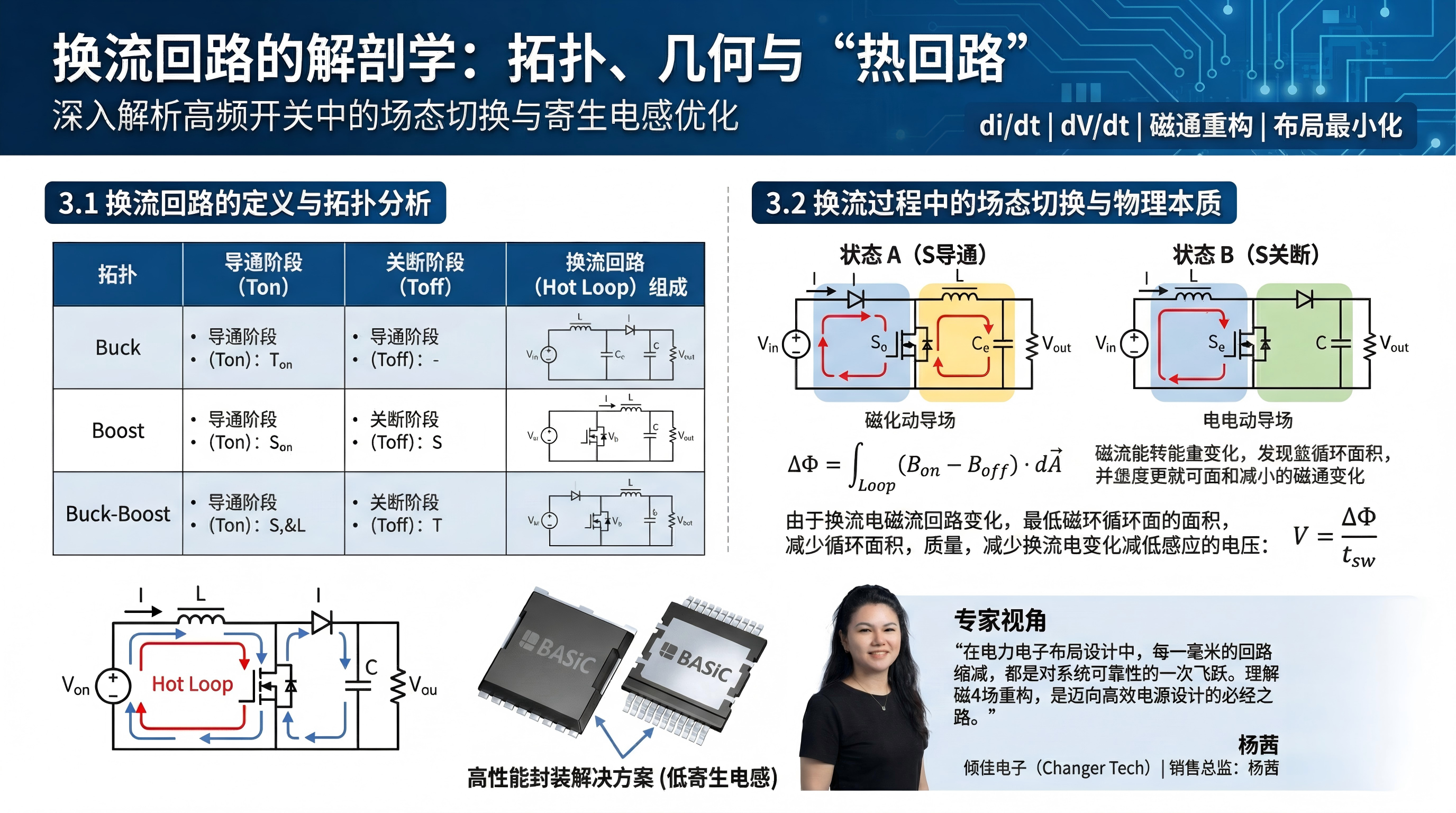
3.1 换流回路的定义

换流回路是指在开关状态切换瞬间，电流从一个支路转移到另一个支路所经过的最小物理路径。它通常包含一个高频开关（如MOSFET/IGBT）、一个续流元件（二极管或同步整流管）和一个高频去耦电容。

拓扑结构	导通阶段 (Ton​) 电流路径	关断阶段 (Toff​) 电流路径	换流回路 (Hot Loop) 组成
Buck (降压)	Cin​→Stop​→L→Load	L→Load→Dbot​→L	Cin​−Stop​−Dbot​
Boost (升压)	L→Sbot​→GND	L→Dtop​→Cout​→GND	Cout​−Dtop​−Sbot​
Buck-Boost	Cin​→S→L	L→D→Cout​	Cin​−S−L−Cout​−D (较为复杂)

3.2 换流过程中的场态切换

以Buck变换器为例，换流过程实际上是两个不同能量场状态的切换：

状态 A (S导通): 输入电容提供能量，电流流经上管。此时，磁场分布围绕着输入电容到上管的路径，电场集中在下管（二极管）两端（反向偏置）。

状态 B (S关断): 上管阻断，电感电流迫使下管导通续流。此时，输入回路的电流迅速降为零，磁场分布转移到下管续流路径，电场集中在上管两端（阻断电压）。

本质分析： 换流回路的物理面积之所以关键，是因为它定义了状态A和状态B之间磁通量变化的区域。

ΔΦ=∫Loop​(Bon​−Boff​)⋅dA

如果回路面积大，意味着在极短的开关时间 tsw​ 内，空间中需要建立或撤销巨大的磁通量 ΔΦ。这需要巨大的能量交换，表现为极大的感应电压 V=ΔΦ/tsw​，这就是为什么PCB布局（Layout）中强调“最小化回路面积”的根本物理原因——即最小化需要重构的磁场体积 。

4. 杂散电感（Stray Inductance）：磁场能量的空间映射

在电路仿真中，杂散电感通常被建模为串联在理想电路中的小电感器。然而，从场论角度看，杂散电感不是一个分立的元件，而是换流回路几何形状与空间磁场相互作用的宏观表现。

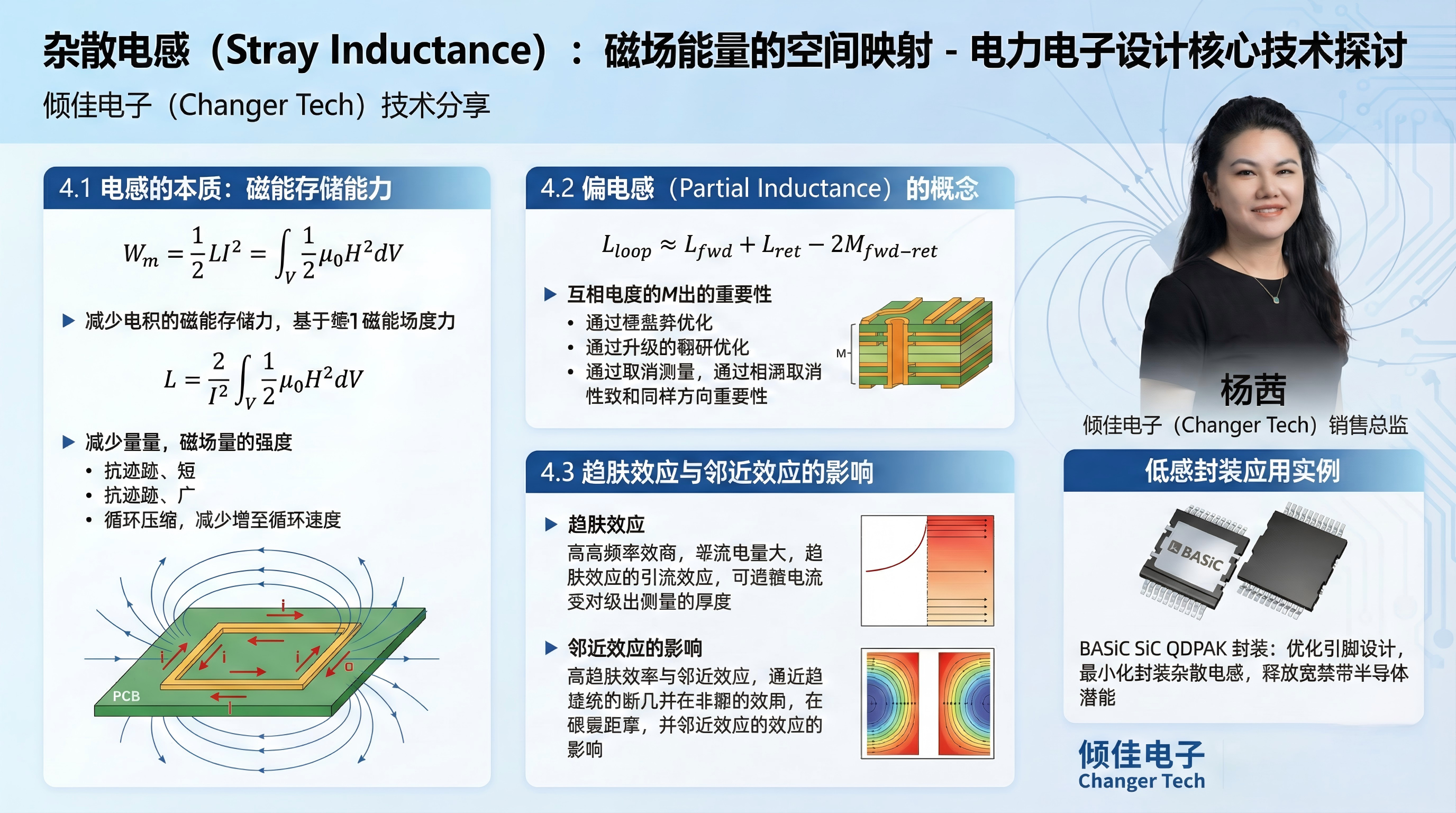
4.1 电感的本质：磁能存储能力

电感的严格定义与磁场能量（Magnetic Energy）直接相关：

Wm​=21​LI2=∫V​21​B⋅HdV

由此可得：

L=I22​∫V​21​μ0​H2dV

这表明，杂散电感 L 正比于单位电流在周围空间中激发的磁场能量总和。

物理推论： 任何能够减少空间磁场体积（Volume）或降低磁场强度（Field Intensity）的措施，都能减小杂散电感。

短走线： 减少了磁场分布的长度，从而减少积分体积 V。

宽走线： 增大了电流流动的截面，降低了附近的磁场密度 H（类似于同轴电缆的外导体屏蔽效应）。

回路面积压缩： 使得往返电流靠得更近，相反方向的磁场在外部空间相互抵消（Flux Cancellation），极大地降低了总磁场能量 。

4.2 偏电感（Partial Inductance）的概念

在复杂的PCB布局中，很难定义一个闭合回路来计算总电感。此时，偏电感概念更为实用。每一段导线片段都有其自身的“自偏电感”（Self Partial Inductance），而任意两段导线之间都有“互偏电感”（Mutual Partial Inductance）。

换流回路的总回路电感 Lloop​ 可表示为：

Lloop​=∑Lself​+∑Mmutual​

对于由去程导体（Forward）和回程导体（Return）组成的回路：

Lloop​≈Lfwd​+Lret​−2Mfwd−ret​

关键洞察： 这一公式揭示了降低换流回路电感的终极秘诀——增强互感 M。通过将PCB的层叠设计（Stack-up）优化，例如将电源层（Power Plane）和地层（Ground Plane）紧密相邻，使得高频电流的回流路径（Return Path）紧贴着去流路径。这使得 Lfwd​ 和 Lret​ 产生的磁场在空间中几乎完全对消，从而将 Lloop​ 降至最低。这就是叠层母排（Laminated Busbar）和多层PCB优越性的电磁场解释 。

4.3 趋肤效应与邻近效应的影响

当频率升高时，导线内部的电流分布不再均匀，这改变了磁场的分布，进而改变了电感值。

趋肤效应（Skin Effect）： 电流集中在导体表面，导线内部磁场减弱，导致**内自感（Internal Inductance）**降低。虽然这对总电感贡献不大（外自感占主导），但显著增加了交流电阻。

邻近效应（Proximity Effect）： 在换流回路中，去程和回程电流方向相反。邻近效应使得电流趋向于集中在两根导线相互靠近的内侧表面。这种“电流挤压”效应实际上进一步减小了电流回路的有效等效面积，从而在极高频下略微降低了回路电感，但代价是极大地增加了铜耗 。

5. 能量流动的真相：坡印廷矢量分析

在电路理论中，我们习惯说“能量通过导线传输”。但这在物理上是错误的。坡印廷定理告诉我们，导线只是能量流动的“导轨”，真正的能量流淌在导线周围的介质（如FR4、空气）中。

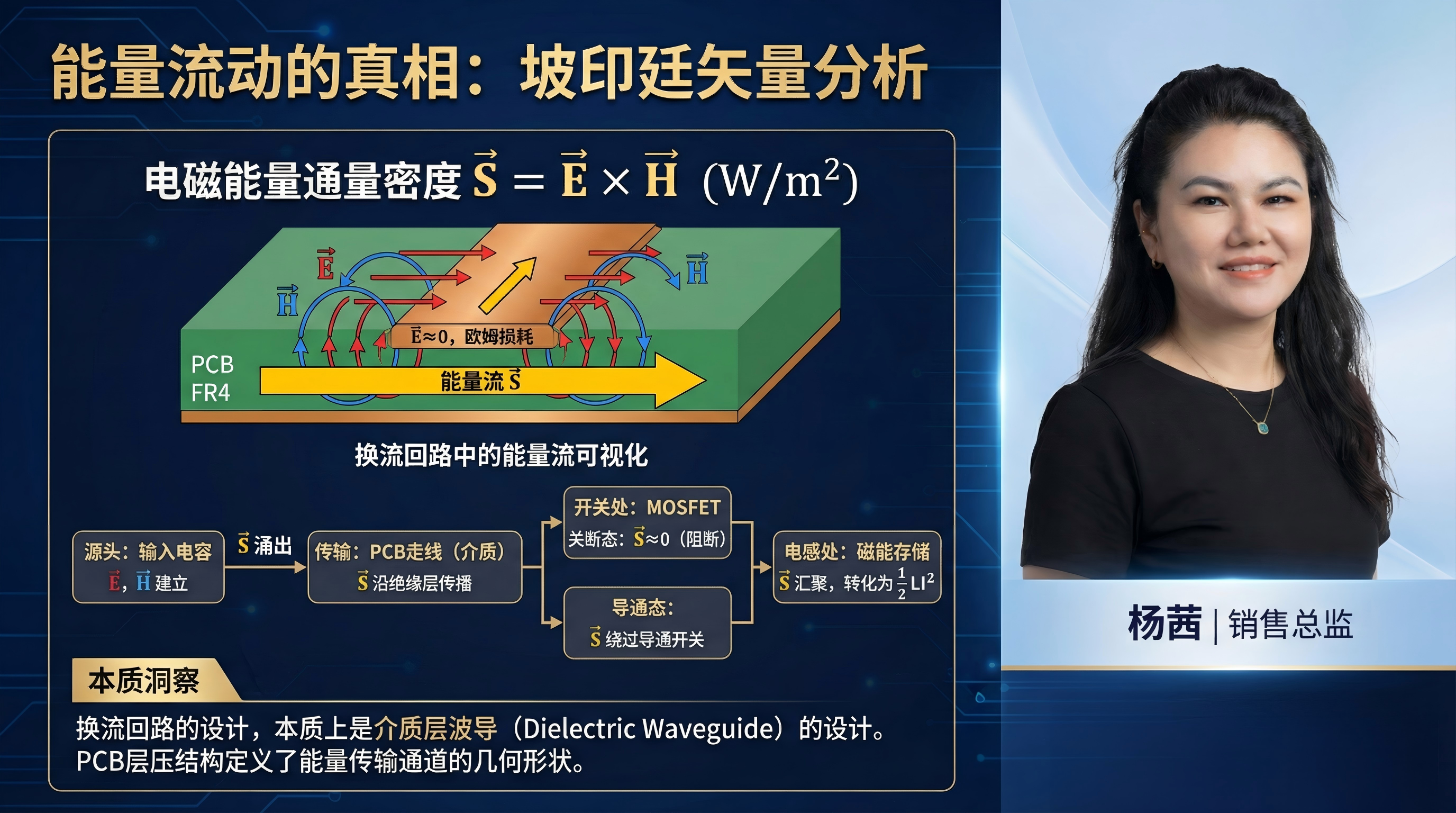
5.1 坡印廷矢量（Poynting Vector）

电磁能量通量密度由坡印廷矢量 S 给出：

S=E×H

单位为瓦特每平方米 (W/m2)。

5.2 换流回路中的能量流可视化

让我们追踪一个MOSFET开通瞬间，能量从输入电容传输到电感的微观过程 ：

源头： 输入电容两端存在高电压（建立强电场 E），电流流出产生磁场 H。在电容介质和周围空间中，E×H 指向负载方向，能量涌出。

传输： 能量流 S 沿着PCB走线（Transmission Line）周围的绝缘层传播。铜箔导线内部由于是良导体，电场 E≈0，因此导线内部几乎没有能量流动（除了少量的欧姆损耗，S 指向导线中心，代表发热）。

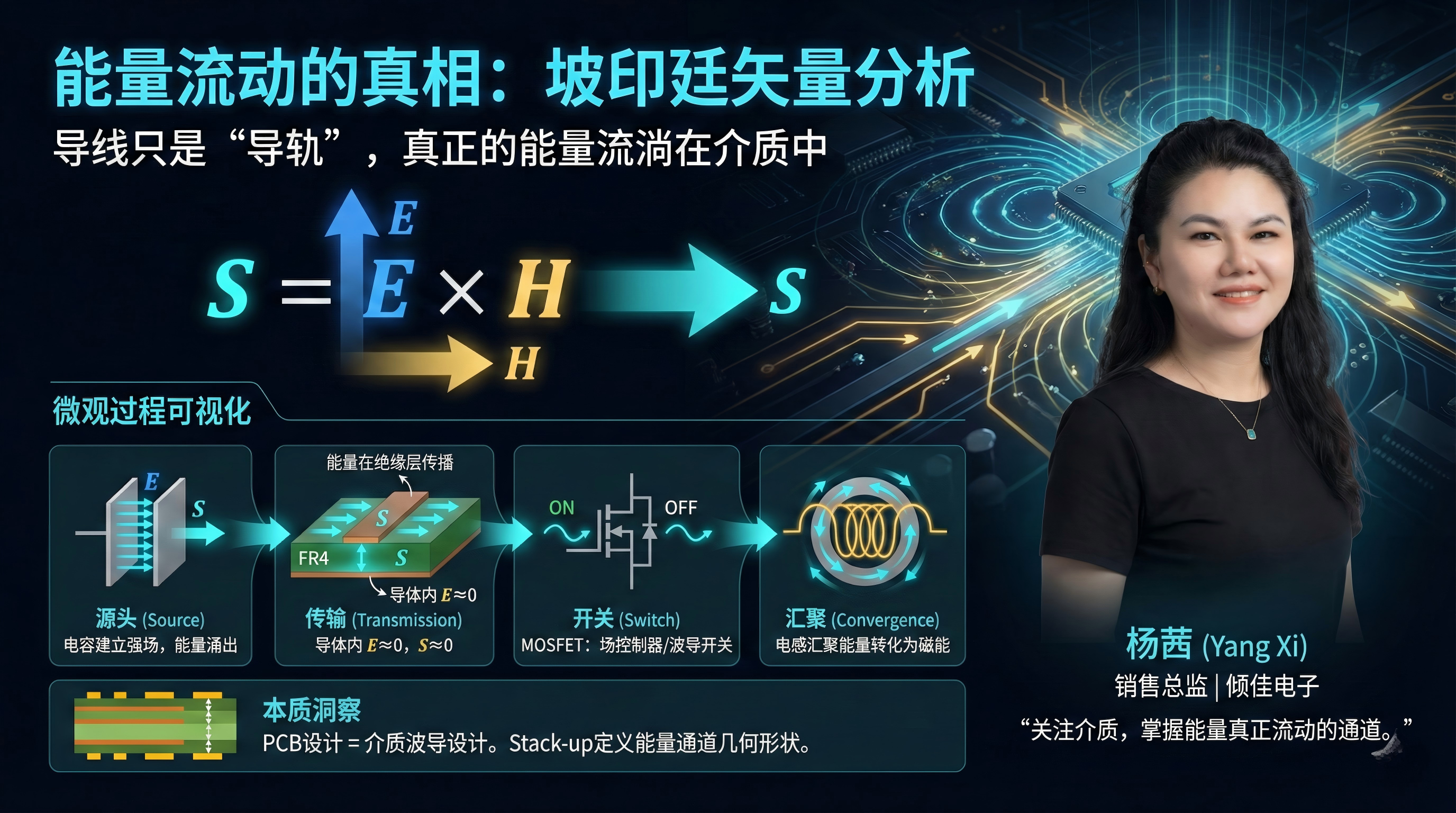
开关处： MOSFET是一个场控制器。

关断态： 漏源极间电压高（E 大），但电流为零（H≈0）。因此 S≈0，能量被阻断，无法通过。

导通态： 漏源极间电压极低（E≈0），电流大（H 大）。理论上理想开关处 S 也较小，这看似矛盾。实际上，能量是绕过导通的开关流动的，或者更准确地说，导通的开关连通了波导结构，使得电磁波能够顺畅地滑过这一区域到达电感。

电感处： 能量流 S 汇聚于电感磁芯。在这里，S 矢量指向磁芯内部，能量被转化为磁能 21​μH 存储起来。

本质洞察： 换流回路的设计，本质上是介质层波导（Dielectric Waveguide）的设计。

如果我们只关注连接铜线而忽略了层间介质厚度、介电常数，就等于忽略了能量真正流动的通道。

PCB层压结构（Stack-up）实际上定义了能量传输通道的几何形状。较薄的介质层厚度（如Core或Prepreg厚度）可以增强电场 E（对于给定电压），但也约束了能量流动的截面，这在传输线理论中对应着降低特征阻抗 Z0​ 。

6. 位移电流（Displacement Current）：共模噪声的幽灵

在低频下可以忽略的位移电流，在高频高压（High Voltage, High Frequency）的电力电子换流中成为了主角，尤其是在分析电磁干扰（EMI）时。

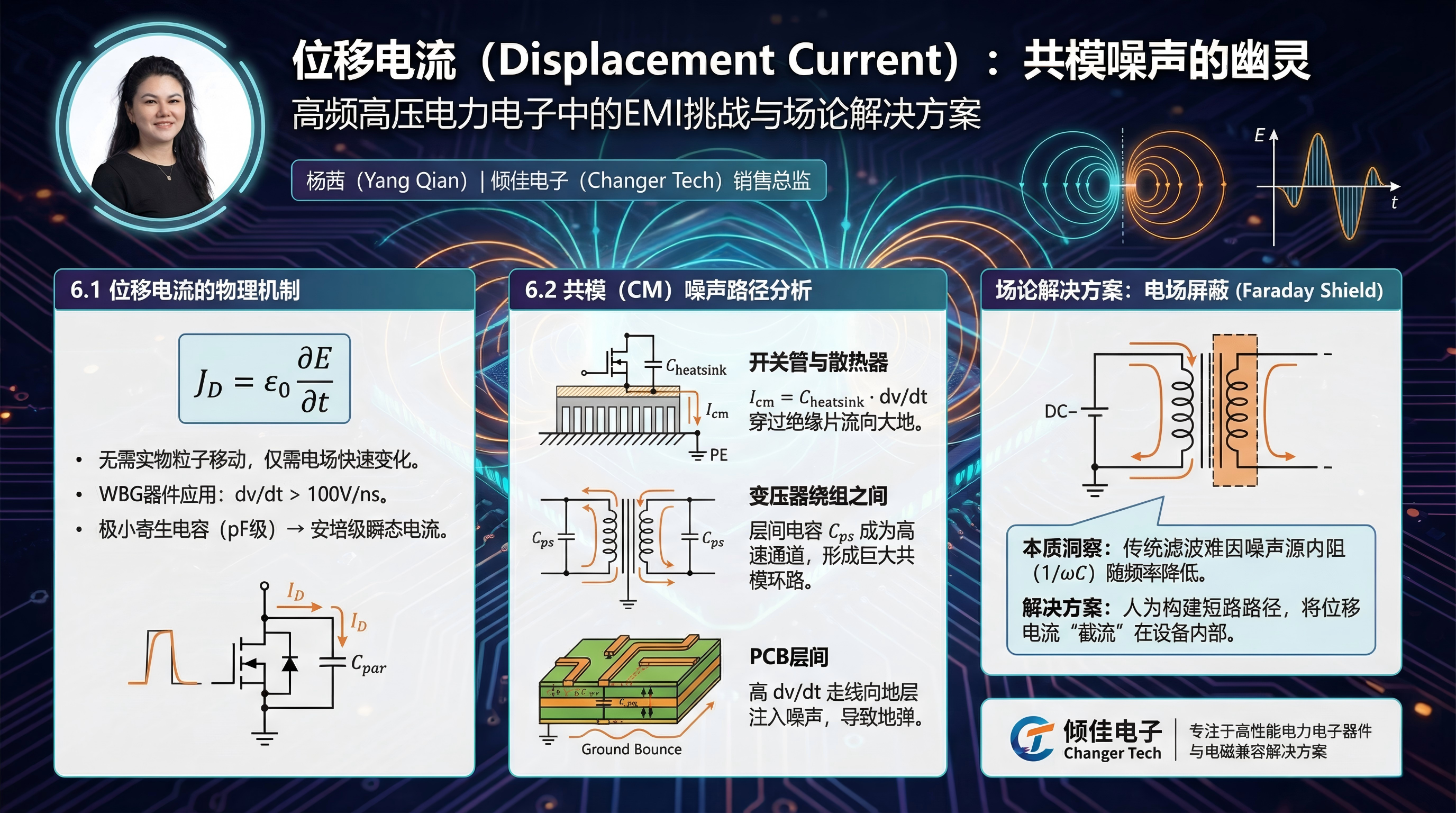
6.1 位移电流的物理机制

位移电流密度定义为：

JD​=ϵ0​∂t∂E​

它不需要任何实物粒子的移动，仅需电场的快速变化。在WBG器件应用中，dv/dt 可高达 100V/ns 甚至更高，这意味着即便通过极小的寄生电容（pF级），也能产生安培级的瞬态电流 。

6.2 共模（CM）噪声路径分析

在典型的隔离型DC/DC变换器或电机驱动系统中，位移电流是共模噪声的主要载体 ：

开关管与散热器之间： MOSFET通常安装在接地的散热器上，中间垫有绝缘片。这构成了一个寄生电容 Cheatsink​。当MOSFET漏极电压以高 dv/dt 跳变时，位移电流 Icm​=Cheatsink​⋅dv/dt 直接穿过绝缘片流向散热器，进而流向大地（PE），形成共模干扰。

变压器绕组之间： 原边绕组连接着高 dv/dt 的开关节点，副边绕组通常连接到静地。原副边之间的层间电容 Cps​ 成为位移电流的高速通道。噪声电流穿过变压器屏障流向副边，再通过输出电缆对地电容流回，形成巨大的共模环路。

PCB层间： 多层PCB中，高 dv/dt 的走线与邻近的参考地层之间也存在分布电容，位移电流会在地层上注入噪声，导致地弹（Ground Bounce）。

本质洞察： 传统的滤波器设计往往难以滤除高频共模噪声，因为噪声源的内阻（由 1/ωC 决定）随频率升高而降低。

场论解决方案： 既然位移电流源于电场耦合，解决之道在于电场屏蔽（Electric Field Shielding） 。例如，在变压器原副边之间插入法拉第屏蔽层（Faraday Shield），并将其连接到原边静点（如直流母线负极）。这样，位移电流就会流向屏蔽层并回流到源头，而不会穿透到副边。这实际上是人为构建了一个短路路径，将位移电流“截流”在设备内部 。

7. 换流回路作为天线：辐射EMI机制

当电流和电压的变化速度极快时，换流回路不仅存储能量，还会向外部空间辐射能量。此时，电路变成了天线。

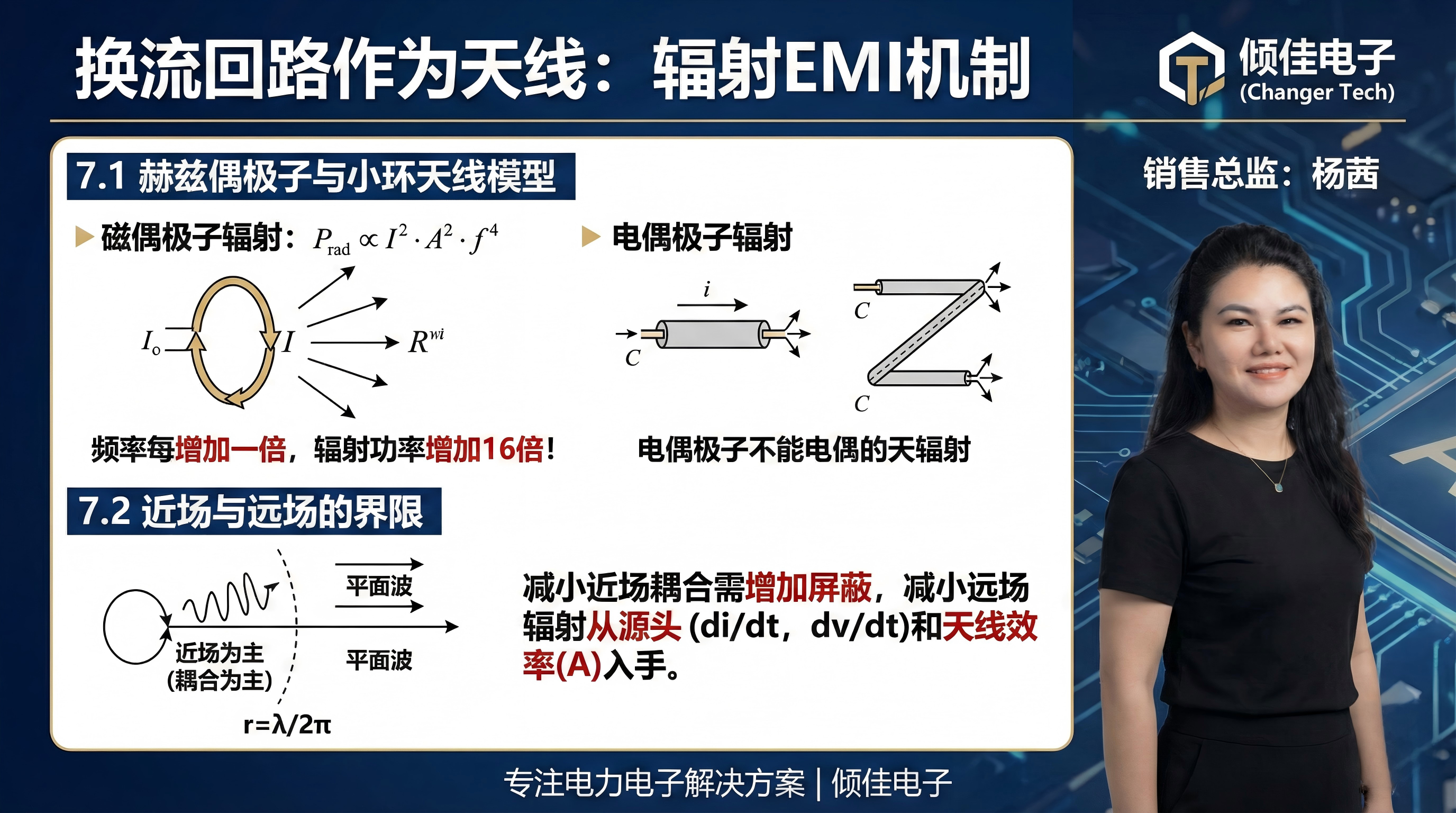
7.1 赫兹偶极子与小环天线模型

换流回路的辐射特性取决于其几何尺寸与波长的比值。在几十MHz的频率下，换流回路通常满足 LoopSize≪λ，可视为电小环天线（Electrically Small Loop Antenna） 。

磁偶极子辐射（Magnetic Dipole Radiation）： 由回路中的差模电流（IDM​）驱动。辐射功率 Prad​ 与回路面积 A 和频率 f 的关系为：

Prad​∝I2⋅A2⋅f4

这意味着，频率每增加一倍，辐射功率增加16倍！这解释了为何WBG器件的高频谐波极其难以处理。

电偶极子辐射（Electric Dipole Radiation）： 由高 dv/dt 节点驱动的共模电流（ICM​）在连接线缆（如输入电源线、输出负载线）上形成驻波，线缆充当了单极子或偶极子天线。由于线缆长度通常远大于PCB回路尺寸，这种辐射往往比磁偶极子辐射强得多 。

7.2 近场与远场的界限

辐射场分为近场（Near Field）和远场（Far Field），分界线通常定义为 r=λ/2π 。

近场区： 电场和磁场相互独立，并未形成稳定的平面波。对于高电流回路，近场以磁场为主（感性）；对于高电压节点，近场以电场为主（容性）。在这一区域，主要的干扰机制是**耦合（Coupling）**而非辐射。

远场区： E 和 H 相互垂直且同相，形成向外传播的电磁波。

本质洞察： 在电力电子设计中，我们主要关注近场耦合对内部电路（如栅极驱动）的影响，以及远场辐射对外部环境（EMC标准）的影响。减小近场耦合需要拉大距离或增加屏蔽；减小远场辐射则必须从源头（减小 di/dt,dv/dt）或天线效率（减小回路面积 A、缩短线缆长度）入手。

8. 传输线效应（Transmission Line Effects）：当导线不再是导线

在SiC应用中，当信号上升时间 tr​ 极短，以至于 tr​<2τprop​（τprop​ 为信号在导线上的传播延迟）时，换流回路中的连接线必须被视为传输线 。

8.1 阻抗不匹配与振荡

传输线具有特征阻抗 Z0​=L′/C′​。如果负载阻抗（例如MOSFET的栅极输入阻抗，可视作电容）与传输线阻抗不匹配，电磁波会在终端发生反射。

反射系数： Γ=ZL​+Z0​ZL​−Z0​​

入射波与反射波叠加，在连接线上形成驻波（Standing Wave）。这表现为栅极电压的剧烈振荡（Ringing），可能导致：

电压过冲击穿栅极氧化层。

电压下冲导致负压超过限制或误关断。

振荡本身成为极强的EMI辐射源 。

8.2 场论指导下的驱动设计

基于传输线理论，解决振荡的本质是阻抗匹配。

源端匹配： 在驱动器输出端串联电阻 Rg​，使得 Rg​+Rdriver​≈Z0​。

开尔文连接（Kelvin Connection）： 从场的角度看，开尔文源极连接实际上是将驱动回路的公共参考点（Common Reference）移除了功率回路的磁通影响范围，实现了控制场域与功率场域的解耦（Decoupling）。

9. 宽禁带（WBG）器件的场效应挑战

宽禁带器件（SiC/GaN）的引入，将上述所有电磁场效应推向了极限。

参数特征	传统 Si IGBT	SiC MOSFET / GaN HEMT	电磁场效应影响
开关频率	5 kHz - 20 kHz	100 kHz - 10 MHz	趋肤效应、邻近效应显著；辐射功率 (P∝f4) 剧增。
开关速度 (dv/dt)	3 - 5 V/ns	50 - 200 V/ns	位移电流 (C⋅dv/dt) 极大增强；共模噪声穿透力极强。
开关速度 (di/dt)	100 - 500 A/μs	1 - 10 A/ns	极小的杂散电感 (L) 也会产生巨大的感应电压 (L⋅di/dt)；近场磁耦合严重。
器件尺寸	较大 (TO-247, Modules)	较小 (SMD, CSP)	功率密度极高，热场与电磁场耦合紧密；散热器成为主要的位移电流通道。

数据整合分析：

在WBG时代，换流回路的“本质”已经从电路参数控制转变为电磁场形态控制。微小的几何布局差异（如几毫米的走线长度差异，或地层平面的完整性）将直接决定变换器是高效运行还是瞬间炸机。

10. 结论与展望：走向多物理场设计

综上所述，电力电子中换流回路的本质，是电磁能量在非理想几何空间中的高频瞬态动力学过程。

电流的二象性： 换流不仅是电子的重定向，更是从传导电流向位移电流的瞬态切换。位移电流揭示了共模噪声如何跨越绝缘介质传播。

能量的空间性： 能量不流经导线，而是流经导线周围的介质。换流回路的设计本质上是构建引导坡印廷矢量流动的波导结构。

电感的几何性： 杂散电感是对空间磁能存储能力的度量。减小电感的唯一途径是压缩磁通体积或利用互感对消。

回路的天线性： 在高频下，任何非闭合的场结构都是天线。EMI的抑制在于控制近场耦合和阻断远场辐射效率。

未来的设计范式

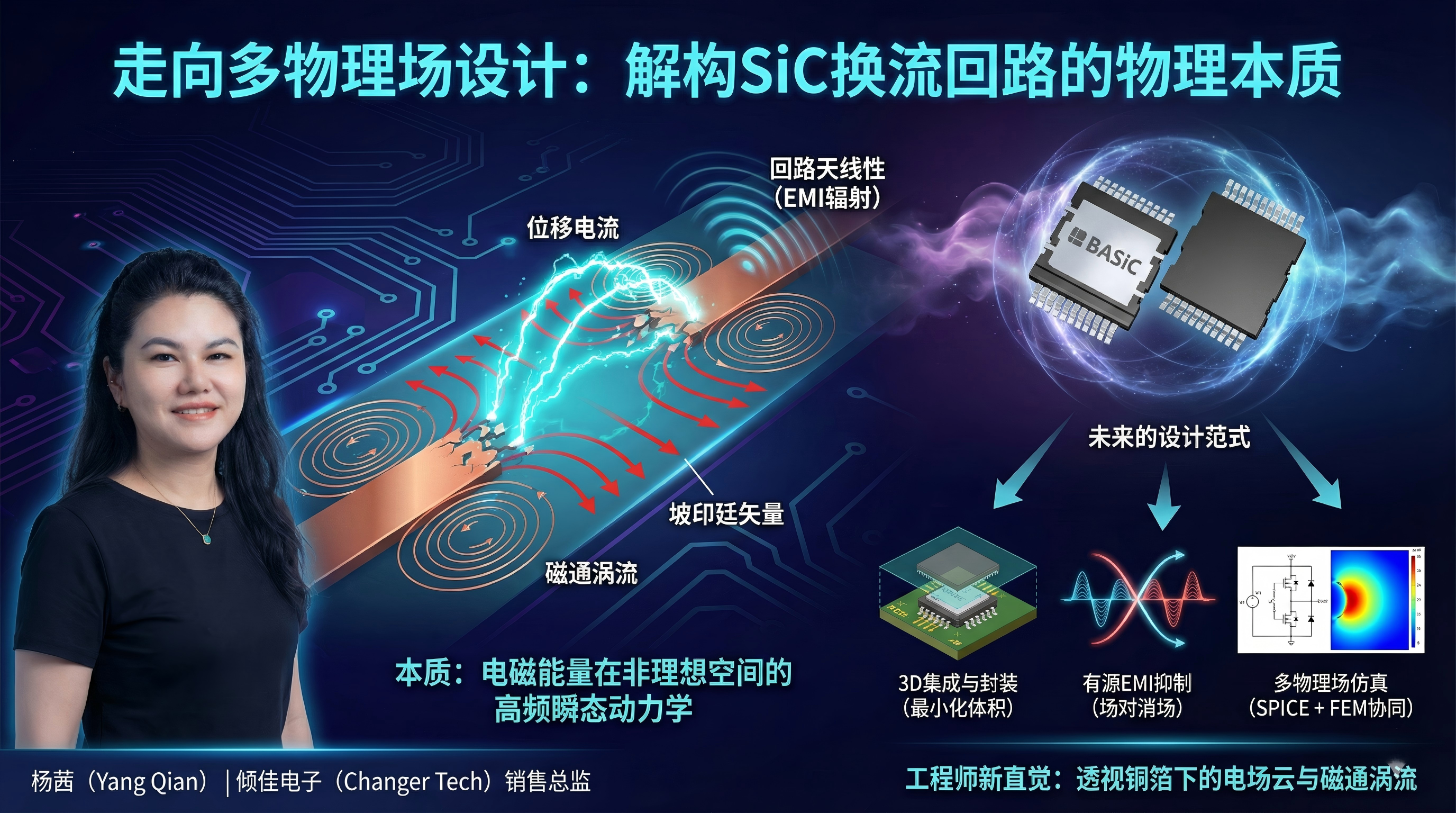
面对电磁场物理本质的挑战，电力电子设计正在经历深刻的变革：

3D集成与封装： 不再区分器件与PCB，而是将芯片嵌入PCB或采用3D异构集成，以最小化换流回路的物理体积 。

有源EMI抑制： 利用反向注入技术产生反相位的电磁场，以“场对消场”的方式抵消噪声，而非仅靠无源滤波。

多物理场仿真（Multi-physics Simulation）： 电路仿真（SPICE）与有限元电磁场仿真（FEM）的协同设计已成为标准流程。

工程师必须具备“场”的直觉——在看到PCB版图时，看到的不仅是铜箔的连接，而是流动的电场云团、旋转的磁通涡流和辐射的电磁波。这才是换流回路的终极物理图景。

审核编辑 黄宇